在△ABC中,∠ABC=45°,tan∠ACB= .如图,把△ABC的一边BC放置在x轴上,有OB=14,OC=
.如图,把△ABC的一边BC放置在x轴上,有OB=14,OC= ,AC与y轴交于点E.21世纪教育网
,AC与y轴交于点E.21世纪教育网
(1)求AC所在直线的函数解析式;
(2)过点O作OG⊥AC,垂足为G,求△OEG的面积;
(3)已知点F(10,0),在△ABC的边上取两点P,Q,是否存在以O,P,Q为顶点的三角形与△OFP全等,且这两个三角形在OP的异侧?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
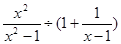 ,再从-2<x<3中选一个合适的整数代入求值。
,再从-2<x<3中选一个合适的整数代入求值。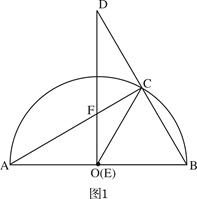
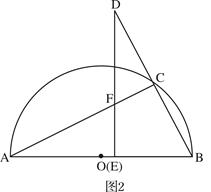
 ≈1.73,
≈1.73, ≈1.41)
≈1.41)

 粤公网安备 44130202000953号
粤公网安备 44130202000953号