学校校园内有一小山坡AB，经测量，坡角∠ABC＝30°，斜坡AB长为12米．为方便学生行走，决定开挖小山坡，使斜坡BD的坡比是1：3(即为CD与BC的长度之比)．A，D两点处于同一铅垂线上，求开挖后小山坡下降的高度AD．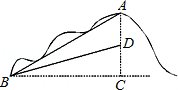
相关试题
，
并写出它的所有整数解．
；
中，
厘米，
厘米（
）．动点
同时从
点出发，分别沿
，
运动，速度是
厘米／秒．过
作直线垂直于
，分别交
，
于
．当点
到达终点
时，点
秒．
厘米，
秒，则
______厘米；
厘米，求时间
，并求出它们的相似比；
与梯形
的面积相等，求
的取值范围；
的面积都相等？若存在，求
相关知识点
推荐套卷
学校校园内有一小山坡AB，经测量，坡角∠ABC＝30°，斜坡AB长为12米．为方便学生行走，决定开挖小山坡，使斜坡BD的坡比是1：3(即为CD与BC的长度之比)．A，D两点处于同一铅垂线上，求开挖后小山坡下降的高度AD．
粤公网安备 44130202000953号