如图，△ABC内接于⊙O，直径BD交AC于E，过O作FG⊥AB，交AC于F，交AB于H，交⊙O于G．
（1）求证：OF•DE=OE•2OH；
（2）若⊙O的半径为12，且OE：OF：OD=2：3：6，求阴影部分的面积．（结果保留根号）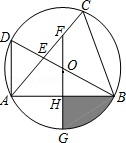
，
．求：
的值；
的值．
，其中
= 
相关知识点
推荐套卷
如图，△ABC内接于⊙O，直径BD交AC于E，过O作FG⊥AB，交AC于F，交AB于H，交⊙O于G．
（1）求证：OF•DE=OE•2OH；
（2）若⊙O的半径为12，且OE：OF：OD=2：3：6，求阴影部分的面积．（结果保留根号）
粤公网安备 44130202000953号