如图，在边长为24cm的正方形纸片ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体形状的包装盒（A．B．C．D四个顶点正好重合于上底面上一点）．已知E、F在AB边上，是被剪去的一个等腰直角三角形斜边的两个端点，设AE=BF=x（cm）．
（1）若折成的包装盒恰好是个正方体，试求这个包装盒的体积V；
（2）某广告商要求包装盒的表面（不含下底面）面积S最大，试问x应取何值？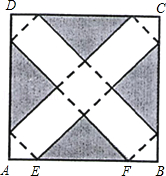
相关试题
( 本题8分) 已知函数
的图象经过点
(- 3, - 2)及点
(1, 6).(1) 求此一次函数解析式,并画图象;
(2) 求此函数图象与坐标轴围成的三角形的面积.
，其中x = -2,y = 
．
相关知识点
推荐套卷
粤公网安备 44130202000953号