如图为7×7的正方形网格,
（1）作出等腰直角三角形ABC关于直线MN成轴对称变换的像⊿A1BC1（A对应A1，C对应C1）；
（2）作出⊿A1BC1绕点B逆时针旋转90o得到的像⊿A2BC2(A1对应A2, C1对应C2)；
（3）填空：⊿A2BC2可以看作将⊿ABC经过连续两次平移得到,则这两次平移具体的操作方法是 ____________________________（需指明每次平移的方向和距离）.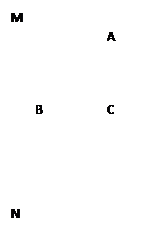
相关试题
如图，已知AB∥CD，∠1：∠2：∠3=1：2：3，求证：BA平分∠EBF．
下面给出证法1．
证法1：∠1、∠2、∠3的度数分别为
，
∵AB∥CD，∴
°，解得
，
∴∠1=36°，∠2=72°，∠3=108°，
∵∠EBD=180°，∴∠EBA=72°，
∴BA平分∠EBF．
请阅读证法1后，找出与证法1不同的证法2，并写出证明过程．
，即
，
的整数部分为2，小数部分为
．
的小数部分为a， 
的小数部分为b，求
的值．
，求
的平方根．相关知识点
推荐套卷
粤公网安备 44130202000953号