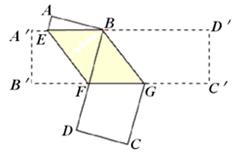
如图，将一张矩形纸片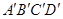
沿EF折叠，使点
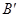落在
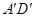边上的点B处；沿BG折叠，使点
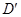落在点D处，且BD过F点.
试判断四边形BEFG的形状，并证明你的结论.
当∠BFE为多少度时，四边形BEFG是菱形.
相关知识点
推荐套卷
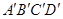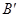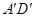如图，将一张矩形纸片沿EF折叠，使点落在 边上的点B处；沿BG折叠，使点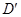落在点D处，且BD过F点.
试判断四边形BEFG的形状，并证明你的结论.
当∠BFE为多少度时，四边形BEFG是菱形.
粤公网安备 44130202000953号