如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.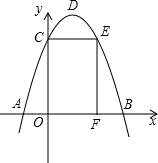
相关知识点
推荐套卷
如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.