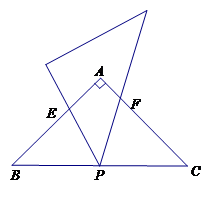
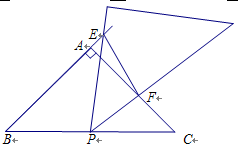
若正整数a、b、c满足方程a2+b2=c2 ,则称这一组正整数(a、b、c)为“商高数”,下面列举五组“商高数”:(3,4,5),(5,12,13),(6,8,10),(7,24,25),(12,16,20),注意这五组“商高数”的结构有如下规律:
根据以上规律,回答以下问题:
(1)商高数的三个数中,有几个偶数,几个奇数?
(2)写出各数都大于30的两组商高数。
(3)用两个正整数m、n(m>n)表示一组商高数,并证明你的结论。
相关知识点
推荐套卷
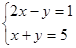
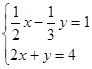 ①②
①②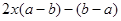
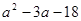
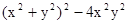
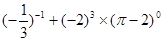
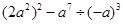
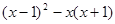
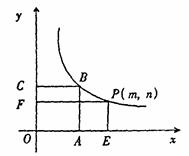
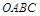 的面积为9 ,点
的面积为9 ,点 在函数
在函数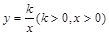 的图象上,点
的图象上,点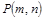 (
(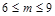 )是函数
)是函数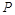 分别作
分别作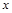 轴、
轴、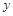 轴的垂线,垂足分别为
轴的垂线,垂足分别为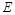 、
、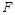 ,若设矩形
,若设矩形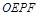 和正方形
和正方形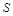 。
。
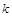 的值;(2)写出
的值;(2)写出 的函数关系和
的函数关系和 粤公网安备 44130202000953号
粤公网安备 44130202000953号