某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如下：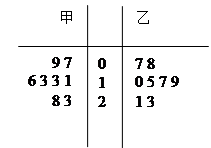
（1）比较这两名队员在比赛中得分的均值和方差的大小；
（2）以上述数据统计甲、乙两名队员得分超过15分的频率作为概率，假设甲、乙两名队员在同一场比赛中得分多少互不影响，预测在本赛季剩余的2场比赛中甲、乙两名队员得分均超过15分的次数
的分布列和均值．
，且
，求
的值.
的终边经过点
，
，求
的值；
且
，求实数
的取值范围.
为锐角，且
，
.
.
平面ABCD，PA=AB=2，且E、F分别是AB、PC的中点.
相关知识点
推荐套卷
某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如下：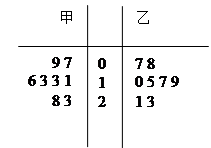
（1）比较这两名队员在比赛中得分的均值和方差的大小；
（2）以上述数据统计甲、乙两名队员得分超过15分的频率作为概率，假设甲、乙两名队员在同一场比赛中得分多少互不影响，预测在本赛季剩余的2场比赛中甲、乙两名队员得分均超过15分的次数的分布列和均值．
粤公网安备 44130202000953号