如图, 已知在平面直角坐标系中，一次函数
(k≠0)的图象与反比例函数
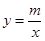(m≠0)的图象相交于A、B两点，且点B的纵坐标为
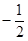，过点A作AC⊥x轴于点C， AC=1,OC=2．
求：（1）求反比例函数和一次函数的关系式；
（2）直接写出反比例函数值大于一次函数值时x的取值范围.
相关知识点
推荐套卷
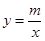如图, 已知在平面直角坐标系中，一次函数(k≠0)的图象与反比例函数(m≠0)的图象相交于A、B两点，且点B的纵坐标为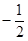，过点A作AC⊥x轴于点C， AC=1,OC=2．
求：（1）求反比例函数和一次函数的关系式；
（2）直接写出反比例函数值大于一次函数值时x的取值范围.
粤公网安备 44130202000953号