数与数之间的关系真奇妙,例如:①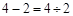 ;②
;② ;③
;③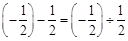 .某教师分析如下:⑴以上这些等式都有一个共同特征:两个实数的差等于这两个实数的商;⑵如果等号左边的第一个实数用
.某教师分析如下:⑴以上这些等式都有一个共同特征:两个实数的差等于这两个实数的商;⑵如果等号左边的第一个实数用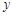 表示,第二个实数用
表示,第二个实数用 表示,则可以得到一个关于
表示,则可以得到一个关于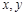 的关系式.请你根据以上分析,再找出一组满足上述特征的两个实数,并写成等式形式: .
的关系式.请你根据以上分析,再找出一组满足上述特征的两个实数,并写成等式形式: .
相关知识点
推荐套卷
数与数之间的关系真奇妙,例如:①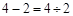 ;②
;② ;③
;③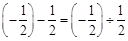 .某教师分析如下:⑴以上这些等式都有一个共同特征:两个实数的差等于这两个实数的商;⑵如果等号左边的第一个实数用
.某教师分析如下:⑴以上这些等式都有一个共同特征:两个实数的差等于这两个实数的商;⑵如果等号左边的第一个实数用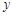 表示,第二个实数用
表示,第二个实数用 表示,则可以得到一个关于
表示,则可以得到一个关于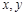 的关系式.请你根据以上分析,再找出一组满足上述特征的两个实数,并写成等式形式: .
的关系式.请你根据以上分析,再找出一组满足上述特征的两个实数,并写成等式形式: .