已知△ABC中，AB＝
，AC＝
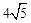，BC＝6．
(1)如图1，点M为AB的中点，在线段AC上取点N，使△AMN与△ABC相似，求线段MN的长；
(2)如图2，是由100个边长为1的小正方形组成的10×10的正方形网格，设顶点在这些小正方形顶点
的三角形为格点三角形．
①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可，不需证明)；
②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数，并画出其中一个(不需
证明)．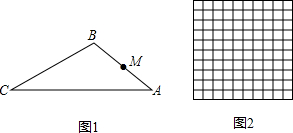
相关试题
在平面直角坐标系中，描出下列各点，并将各点用线段依次连接起来：
（1，1）（6，1）（6，3）（7，3）（4，6）（1，3）（2，3）
观察得到的图形，你觉得它像什么？
，
，若点
为直线
上的任意一点，则点
，
，
，
，
，
．
的边长为6，建立适当的平面直角坐标系，分别表示
，
，
，
四个点的坐标．
相关知识点
推荐套卷
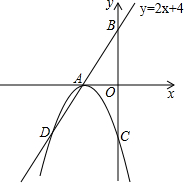
粤公网安备 44130202000953号