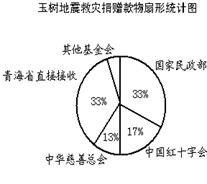
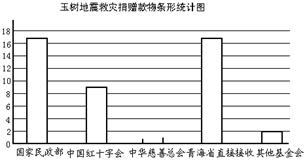
玉树地震后,全国人民慷慨解囊,积极支援玉树人民抗震救灾,他们有的直接捐款,有的捐物.国家民政部、中国红十字会、中华慈善总会及其他基金会分别接收了捐赠,青海省也直接接收了部分捐赠.截至5月14日12时,他们分别接收捐赠(含直接捐款数和捐赠物折款数)的比例见扇形统计图(图①),其中,中华慈善总会和中国红十字会共接收捐赠约合人民币15.6亿元.请你根据相关信息解决下列问题:
(1)其他基金会接收捐赠约占捐赠总数的百分比是;
(2)全国接收直接捐款数和捐物折款数共计约亿元;
(3)请你补全图②中的条形统计图;
(4)据统计,直接捐款数比捐赠物折款数的6倍还多3亿元,那么直接捐款数和捐赠物折款数各多少亿元?