已知一次函数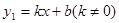 的图象与反比例函数
的图象与反比例函数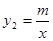 (
(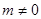 )的图象交于
)的图象交于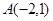 、
、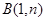 两点。
两点。
(1)求反比例函数和一次函数的解析式,求出点B的坐标;
(2)在同一坐标系中画出两个函数的图像的示意图,并观察图像回答:当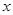 为何值时,
为何值时,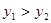 ?
?
(3)已知点C(1,0),求出△ABC的面积。
(4)在BC上是否存在一点E,使得直线AE将△ABC的面积二等分,如果存在请你画出这条直线,求出点E的坐标;如果不存在,请简单说明理由。
相关知识点
推荐套卷
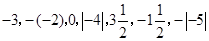
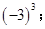 (2)
(2) (3)
(3) (4)
(4)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号