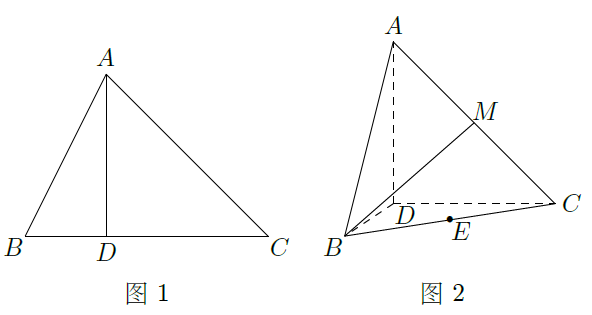
如图1,
,过动点
作
,垂足
在线段
上且异于点
,连接
,沿
将
折起,使
(如图2所示).
(Ⅰ)当
的长为多少时,三棱锥
的体积最大;
(Ⅱ)当三棱锥
的体积最大时,设点
分别为棱
的中点,试在棱
上确定一点
,使得
,并求
与平面
所成角的大小.
推荐套卷
如图1,
,过动点
作
,垂足
在线段
上且异于点
,连接
,沿
将
折起,使
(如图2所示).
(Ⅰ)当
的长为多少时,三棱锥
的体积最大;
(Ⅱ)当三棱锥
的体积最大时,设点
分别为棱
的中点,试在棱
上确定一点
,使得
,并求
与平面
所成角的大小.
