操作：如图，在正方形ABCD中，P是CD上一动点（与C、D不重合），使三角板的直角顶点与点P重合，并且一条直角边始终经过点B，另一直角边与正方形的某一边所在直线交于点E．
探究：①观察操作结果，哪一个三角形与△BPC相似，写出你的结论，（找出两对即可）；并选择其中一组说明理由；
②当点P位于CD的中点时，直接写出① 中找到的两对相似三角形的相似比和面积比．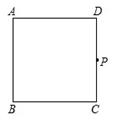
=
，且2a－b+3c=21，试求a∶b∶c.
，求线段PQ的长.相关知识点
推荐套卷
操作：如图，在正方形ABCD中，P是CD上一动点（与C、D不重合），使三角板的直角顶点与点P重合，并且一条直角边始终经过点B，另一直角边与正方形的某一边所在直线交于点E．
探究：①观察操作结果，哪一个三角形与△BPC相似，写出你的结论，（找出两对即可）；并选择其中一组说明理由；
②当点P位于CD的中点时，直接写出① 中找到的两对相似三角形的相似比和面积比．
粤公网安备 44130202000953号