先阅读下面解方程 的过程,然后回答后面的问题。
的过程,然后回答后面的问题。
解:将原方程整理为: (第一步)
(第一步)
方程两边同除以(x-1)得: 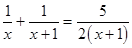 (第二步)
(第二步)
去分母,得:2(x+1)+2x=5x(第三步)
解这个方程,得:x=2(第四步)
在上面的解题过程中:第三步变形的依据是
出现错误的一步是
上述解题过程缺少的一步是
写出这个方程的完整的解题过程
先阅读下面解方程 的过程,然后回答后面的问题。
的过程,然后回答后面的问题。
解:将原方程整理为: (第一步)
(第一步)
方程两边同除以(x-1)得: 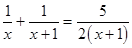 (第二步)
(第二步)
去分母,得:2(x+1)+2x=5x(第三步)
解这个方程,得:x=2(第四步)
在上面的解题过程中:第三步变形的依据是
出现错误的一步是
上述解题过程缺少的一步是
写出这个方程的完整的解题过程