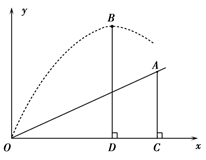
小明在一次高尔夫球比赛中，从山坡下的O点打出一记球向山坡上的球洞A点飞去，球的飞行路线为抛物线. 如果不考虑空气阻力，当球飞行的水平距离为9米时，球达到最大水平高度为12米．已知山坡OA与水平方向的夹角为30o，O、A两点相距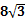 
米．请利用下面所给的平面直角坐标系探索下列问题：
（1）求出点A的坐标；
（2）判断小明这一杆能否把高尔夫球从O点直接打入球洞A点，并说明理由．
．
。
．
，若代数式
化简的结果为
，请你求出满足条件的a值．
，求代数式（a - 1）2 + b（2a + b）+ 2a 的值．相关知识点
推荐套卷
小明在一次高尔夫球比赛中，从山坡下的O点打出一记球向山坡上的球洞A点飞去，球的飞行路线为抛物线. 如果不考虑空气阻力，当球飞行的水平距离为9米时，球达到最大水平高度为12米．已知山坡OA与水平方向的夹角为30o，O、A两点相距 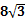米．请利用下面所给的平面直角坐标系探索下列问题：
（1）求出点A的坐标；
（2）判断小明这一杆能否把高尔夫球从O点直接打入球洞A点，并说明理由．
粤公网安备 44130202000953号