某水果公司以2元/千克的成本购进10000千克柑橘，销售人员在销售过程中随
机抽取柑橘进行“柑橘损坏率”统计，并绘制成如图5所示的统计图，根据统计图提供的信
息解决下面问题：
⑴ 柑橘损坏的概率估计值为 ，柑橘完好的概率估计值为 ；
⑵ 估计这批柑橘完好的质量为 千克；
⑶ 如果公司希望销售这些柑橘能够获得25000元的利润，那么在出售(已去掉损坏的柑橘)时，每千克柑橘大约定价为多少元比较合适？
相关试题
的三个顶点均在格点上，点A、B的坐标分别为
后的
；
的坐标；
的面积.
的方程为
．一道选择题共有A、B、C、D四个备选答案，
（1）如果其中只有一个是正确的，某位同学随意选了其中一个答案，他选中正确答案的概率是多少？
（2）如果其中有两个是正确的，某位同学随意选了其中两个答案，他选中正确答案的概率是多少？
，另一边所在直线与半圆相交于点
，量出半径
，弦
，求直尺的宽度．
相关知识点
推荐套卷
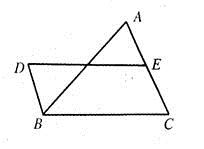
粤公网安备 44130202000953号