已知函数
满足：①定义在
上；②当
时，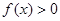
；③对于任意的
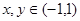，有
.
（1）取一个对数函数
，验证它是否满足条件②，③；
（2）对于满足条件①，②，③的一般函数，判断是否具有奇偶性和单调性，并加以证明.
，求经过圆上一点
的切线方程．
中，
，
，
平面
，
，
分别是
上的动点，且
：
为何值，总有平面
平面
；
？ 
中，底面
是矩形，
平面
分别是
的中点，
．
平面
；
⊥平面
．
,求x2+y2的最值.
表示的平面区域.
相关知识点
推荐套卷
已知函数满足：①定义在上；②当时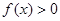，；③对于任意的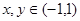，有.
（1）取一个对数函数，验证它是否满足条件②，③；
（2）对于满足条件①，②，③的一般函数，判断是否具有奇偶性和单调性，并加以证明.
粤公网安备 44130202000953号