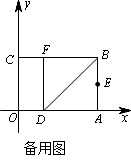
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为 顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周 长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
相关知识点
推荐套卷
 的解为坐标的点在平面直角坐标系中的图象是一条直线。根据这个结论,在同一平面直角坐标系中画出二元一次方程组
的解为坐标的点在平面直角坐标系中的图象是一条直线。根据这个结论,在同一平面直角坐标系中画出二元一次方程组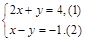 中两个二元一次方程的图象,并根据图象写出这个二元一次方程组的解。
中两个二元一次方程的图象,并根据图象写出这个二元一次方程组的解。 粤公网安备 44130202000953号
粤公网安备 44130202000953号