某市为准备参加省中学生运动会,对本市甲、乙两个田径队的所有跳高运动员进行了测试,用茎叶图表示出甲、乙两队运动员本次测试的跳高成绩(单位:cm,且均为整数),同时对全体运动员的成绩绘制了频率分布直方图.跳高成绩在185cm以上(包括185cm)定义为“优秀”,由于某些原因,茎叶图中乙队的部分数据丢失,但已知所有运动员中成绩在190cm以上(包括190cm)的只有两个人,且均在甲队.
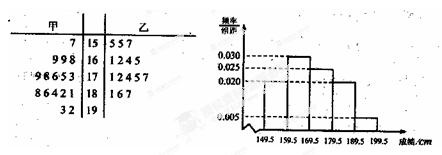
(Ⅰ)求甲、乙两队运动员的总人数a及乙队中成绩在[160,170)(单位:cm)内的运动员人数b;
(Ⅱ)在甲、乙两队所有成绩在180cm以上的运动员中随机选取2人,已知至少有1人成绩为“优秀”,
求两人成绩均“优秀”的概率;
(Ⅲ)在甲、乙两队中所有的成绩为“优秀”的运动员中随机选取2人参加省中学生运动会正式比赛,
求所选取运动员中来自甲队的人数X的分布列及期望.