已知椭圆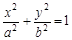
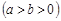的离心率为
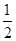，两焦点之间的距离为4．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）过椭圆的右顶点作直线交抛物线
于A、B两点，
（1）求证：OA⊥OB；
（2）设OA、OB分别与椭圆相交于点D、E，过原点O作直线DE的垂线OM，垂足为M，证明|OM|为定值．
相关试题
的定义域为R,求
的值域.
，
是两个不共线的向量，且
，
．
与
垂直；
，
，且
，求
的值．
（
是常数）是奇函数，且满足
.
在区间
上的单调性并说明理由.
推荐套卷
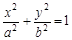
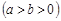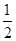已知椭圆的离心率为，两焦点之间的距离为4．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）过椭圆的右顶点作直线交抛物线于A、B两点，
（1）求证：OA⊥OB；
（2）设OA、OB分别与椭圆相交于点D、E，过原点O作直线DE的垂线OM，垂足为M，证明|OM|为定值．
粤公网安备 44130202000953号