(本小题满分12分)函数f(x)=ax2-2(a-1)x-2lnx ,a>0
(1)求函数f(x)的单调区间;
(2)对于函数图像上的不同两点A(x1,y1),B(x2,y2),如果在函数图像上存在点P(x0,y0)(其中x0在x1与x2之间),使得点P处的切线l平行于直线AB,则称AB存在“伴随切线”,当x0= 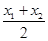 时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由
时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由
推荐套卷
(本小题满分12分)函数f(x)=ax2-2(a-1)x-2lnx ,a>0
(1)求函数f(x)的单调区间;
(2)对于函数图像上的不同两点A(x1,y1),B(x2,y2),如果在函数图像上存在点P(x0,y0)(其中x0在x1与x2之间),使得点P处的切线l平行于直线AB,则称AB存在“伴随切线”,当x0= 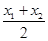 时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由
时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由