某中学开展以“三创一办”为中心,以“校园文明”为主题的手抄报比赛.同学们积极参与,参赛同学每人交了一份得意作品,所有参赛作品均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,将获奖结果绘制成如下两幅统计图.请你根据图中所给信息解答下列问题:
各奖项人数百分比统计图 各项奖人数统计图
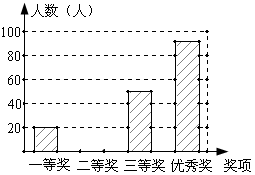
(1)一等奖所占的百分比是______;
(2)在此次比赛中,一共收到多少份参赛作品?请将条形统计图补充完整;
(3)各奖项获奖学生分别有多少人?
相关知识点
推荐套卷
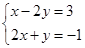 ;②
;②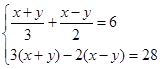
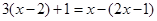 ;②
;②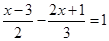
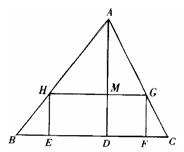
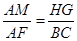 ;
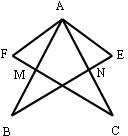
;
 ,AD为中线,求sin∠CAD的值.
,AD为中线,求sin∠CAD的值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号