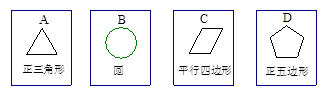有四张背面相同的纸牌A，B，C，D，其正面分别画有四个不同的几何图形（如图）．小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．
用树状图(或列表法)表示两次摸牌所有可能出现的结果（纸牌可用A，B，C，D表示）；
求摸出两张牌面图形都是中心对称图形的纸牌的概率．
相关试题
；
．
。（n为正整数）
CD于E， PF
BC，E为BC的中点，求证：AB=2DE
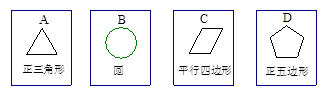
相关知识点
推荐套卷
有四张背面相同的纸牌A，B，C，D，其正面分别画有四个不同的几何图形（如图）．小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．
用树状图(或列表法)表示两次摸牌所有可能出现的结果（纸牌可用A，B，C，D表示）；
求摸出两张牌面图形都是中心对称图形的纸牌的概率．
粤公网安备 44130202000953号