将矩形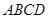 纸片沿对角线
纸片沿对角线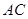 剪开,得
剪开,得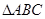 和
和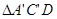 ,如图(1-1)所示.将
,如图(1-1)所示.将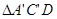 的顶点
的顶点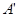 与点
与点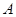 重合,并绕点
重合,并绕点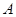 按逆时针方向旋转,使点
按逆时针方向旋转,使点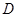 、
、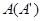 、
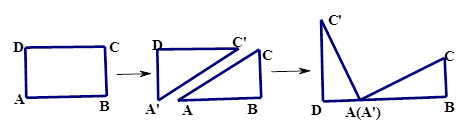
、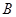 在同一条直线上,如图(1-2)所示.
在同一条直线上,如图(1-2)所示.观察图可知:与BC相等的线段是______,
 =_______;
=_______;
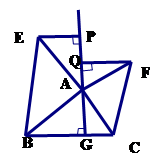
如图(2),
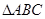 中,
中,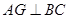 于点
于点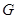 ,以
,以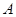 为直角顶点,分别以
为直角顶点,分别以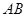 、
、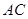 为直角边,向
为直角边,向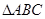 外作等腰
外作等腰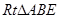 和等腰
和等腰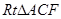 ,过点
,过点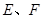 作射线
作射线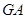 的垂线,垂足分别为
的垂线,垂足分别为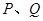 . 求证:
. 求证: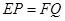 .
.
如图(3),
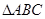 中,
中,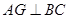 于点
于点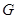 ,以
,以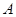 为直角顶点,分别以
为直角顶点,分别以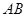 、
、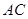 为直角边,向
为直角边,向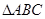 外作
外作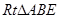 和
和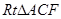 ,过点
,过点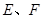 作射线
作射线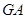 的垂线,垂足分别为
的垂线,垂足分别为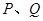 .若
.若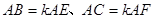 ,试探究
,试探究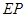 与
与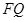 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
相关知识点
推荐套卷

 粤公网安备 44130202000953号
粤公网安备 44130202000953号