去年寒假期间，学校团委要求学生参加一项社会调查活动，八年级学生小青想了解她所在的小区500户居民家庭月人均收入情况，从中随机调查了一定数量的居民家庭的月人均收入（元）情况，并绘制成如下的频数分布直方图（每组含左端点，不含右端点）和扇形统计图．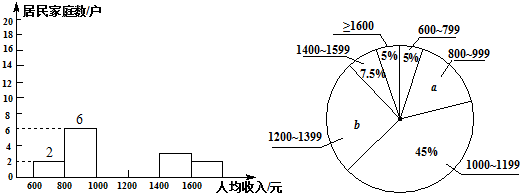
请你根据以上不完整的频数分布直方图和扇形统计图提供的信息，解答下列问题：这次共调查了多少户居民家庭的人均收入？扇形统计图中的a=，b= ；．
补全频数分布直方图．
先阅读理解下面的例题，再按要求解答后面的问题
例题：解一元二次不等式
＞0.解：令y=，画出y=如图所示，
由图像可知：当x＜1或x＞2时，y＞0.所以一元二次不等式＞0的解集为x＜1或x＞2.
填空：（1）
＜0的解集为；
（2）
＞0的解集为；
用类似的方法解一元二次不等式
＞0.
如图，在矩形ABCD（AB＜AD）中，将△ABE沿AE对折，使AB边落在对角线AC上，点B的对应点为F，同时将△CEG沿EG对折，使CE边落在EF所在直线上，点C的对应点为H．
（1）证明：AF∥HG（图（1））；
（2）如果点C的对应点H恰好落在边AD上（图（2））．判断四边形AECH的形状，并说明理由．
甲、乙两人准备整理一批新到的实验器材．若甲单独整理需要40分钟完工；若甲、乙 共同整理20分钟后，乙需再单独整理20分钟才能完工．
（1）问乙单独整理多少分钟完工？
（2）若乙因工作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？
要了解某地区九年级学生的身高情况，从中随机抽取
名学生的身高作为一个样本，身高均在
～
之间（取整数厘米），整理后分成
组，绘制出频数分布直方图（不完整）．根据图中提供的信息，解答下列问题：
（1）补全频数分布直方图；
（2）抽取的样本中，学生身高的中位数在哪个小组？
（3）该地区共有
名九年级学生，估计其中身高不低于
的人数．
看地面
、
两点，测得它们的俯角分别是
和
．已知
，
、
．（精确到
，参考数据：
，
）
粤公网安备 44130202000953号