如图9, 已知抛物线与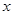
轴交于A (－4，0) 和B(1，0)两点，与
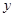轴交于C（0，-2）点．求此抛物线的解析式；
设G是线段BC上的动点，作GH//AC交AB于H，连接CF，当△BGH的面积是△CGH面积的3倍时，求H点的坐标;
若M为抛物线上A、C两点间的一个动点，过M作
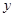轴的平行线，交AC于N，当M点运动到什么位置时，线段MN的值最大，并求此时M点的坐标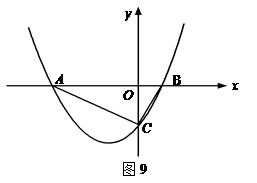
的方程
和方程
的解相同，求
的值。
相关知识点
推荐套卷
如图9, 已知抛物线与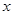轴交于A (－4，0) 和B(1，0)两点，与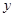轴交于C（0，-2）点．求此抛物线的解析式；
设G是线段BC上的动点，作GH//AC交AB于H，连接CF，当△BGH的面积是△CGH面积的3倍时，求H点的坐标;
若M为抛物线上A、C两点间的一个动点，过M作
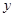轴的平行线，交AC于N，当M点运动到什么位置时，线段MN的值最大，并求此时M点的坐标
粤公网安备 44130202000953号