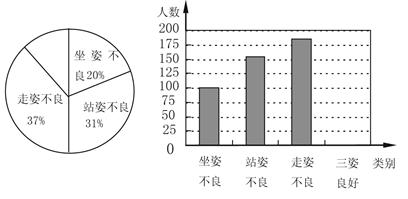
国民体质监测中心等机构开展了青少年形体测评.专家组随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:请将两幅统计图补充完整;
在这次形体测评中,一共抽查了 名学生,如果全市有10万名初中生,那么全市初中生中,三姿良好的学生约有 人;
根据统计结果,请你简单谈谈自己的看法.
相关知识点
推荐套卷

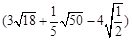 ÷
÷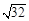 ;(2)分解因式
;(2)分解因式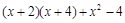 .
. 中,已知二次函数
中,已知二次函数 的图象经过点
的图象经过点 和点
和点 ,直线
,直线 经过抛物线的顶点且与
经过抛物线的顶点且与 轴垂直,垂足为
轴垂直,垂足为 .
. 从点
从点 处出发沿抛物线向上运动,其纵坐标
处出发沿抛物线向上运动,其纵坐标 随时间
随时间 ≥
≥ )的变化规律为
)的变化规律为 .现以线段
.现以线段 为直径作
为直径作 .
. 随时间
随时间 的变化规律为
的变化规律为 ,则当
,则当 ,试求
,试求 的最大值.
的最大值.
 且
且 时,因为
时,因为 ≥
≥ ,所以
,所以 ≥
≥ ≥
≥ (当
(当 时取等号).
时取等号). ,由上述结论可知:当
,由上述结论可知:当 与函数
与函数 , 则当
, 则当 ____时,
____时, 取得最小值为___.
取得最小值为___. 与函数
与函数 ,求
,求 的最小值,并指出取得
的最小值,并指出取得 的值.
的值. 元;二是燃油费,每千
元;二是燃油费,每千 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为 .设该汽车一次运输的路
.设该汽车一次运输的路 千米,求当
千米,求当 粤公网安备 44130202000953号
粤公网安备 44130202000953号