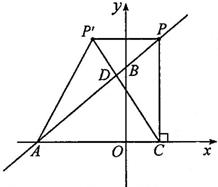
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P´(点P´不在y轴上),连接PP´,P´A,P´C.设点P的横坐标为a.
(1)当b=3时,
①求直线AB的解析式;
②若点P′的坐标是(﹣1,m),求m的值;
(2)若点P在第一象限,记直线AB与P´C的交点为D.当P´D:DC=1:3时,求a的值;
(3)是否同时存在a,b,使△P´CA为等腰直角三角形?若存在,请求出所有满足要求的a,b的值;若不存在,请说明理由.