如图1,二次函数y=ax2+bx+c(a≠0)的图像与x轴交于点A、点B,与y轴交于点C,且A、B两点的坐标分别是(4,0)、(0,-2),tan∠BCO=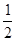 (1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.
(1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.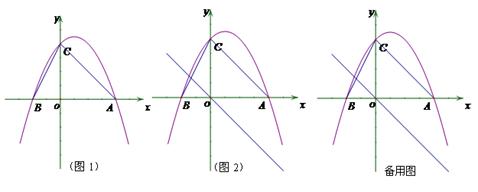
相关知识点
推荐套卷
 与x的
与x的 的和是非负数
的和是非负数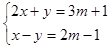 ,试列出使x>y成立的关于m的不等式.
,试列出使x>y成立的关于m的不等式. 粤公网安备 44130202000953号
粤公网安备 44130202000953号