如图1,抛物线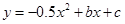 与x轴交于B(3,0) 、C(8.0)两点,抛物线另有一点A在第一象限内,连接AO、AC,且AO=AC.
与x轴交于B(3,0) 、C(8.0)两点,抛物线另有一点A在第一象限内,连接AO、AC,且AO=AC.求抛物线的解析式;
将△OAC绕x轴旋转一周,求所得旋转体的表面积;
如图2,将△OAC沿x轴翻折后得△ODC,设垂直于x轴的直线l:x=n与(1)中所求的抛物线交于点M,与CD交于点N,若直线l 沿x轴方向左右平移,且交点M始终位于抛物线上A、C两点之间时,试探究:当n为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.
相关知识点
推荐套卷
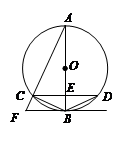
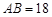 ,
, ,求弦CD的长;
,求弦CD的长;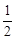 ,你赞成他的观点吗?请用列表法或画树形图法分析说明.
,你赞成他的观点吗?请用列表法或画树形图法分析说明.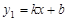 的图象与反比例函数
的图象与反比例函数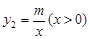 的图象交于A(1,6),B(
的图象交于A(1,6),B(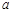 ,2)两点.
,2)两点.
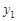 ≥
≥ 时
时 的取值范围.
的取值范围.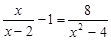 .
. 的顶点为P,与
的顶点为P,与 轴交于点A,与直线OP交于点B.
轴交于点A,与直线OP交于点B. ,求点M的坐标;
,求点M的坐标; 轴于点D.将抛物线
轴于点D.将抛物线
 粤公网安备 44130202000953号
粤公网安备 44130202000953号