已知等腰△ABC中，AB=AC，D是BC的中点，将三角板中的90°角的顶点绕D点在△ABC内旋转，角的两边分别与AB、AC交于E、F，且点E、F不与A、B、C三点重合．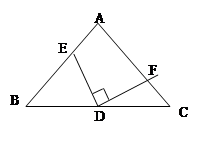
如果∠A=90°求证：DE=DF
如果DF//AB，则结论：“四边形AEDF为直角梯形”是否正确，若正确，请证明；若不正确，请画出草图举反例
相关知识点
推荐套卷
已知等腰△ABC中，AB=AC，D是BC的中点，将三角板中的90°角的顶点绕D点在△ABC内旋转，角的两边分别与AB、AC交于E、F，且点E、F不与A、B、C三点重合．如果∠A=90°求证：DE=DF
如果DF//AB，则结论：“四边形AEDF为直角梯形”是否正确，若正确，请证明；若不正确，请画出草图举反例
粤公网安备 44130202000953号