红星中学开展了“绿化家乡,植树造林 ”活动,并对该校的甲、乙、丙、丁四个班级种树情况进行了考察,并将收集的数据绘制了图①和图②两幅尚不完整的统计图.
请根据图中提供的信息,完成下列问题: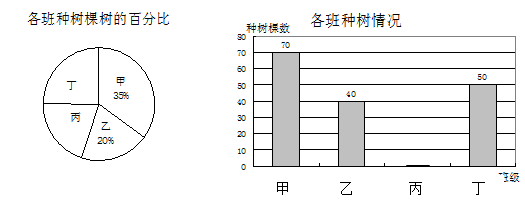
这四个班共种__▲______棵树.
请你补全两幅统计图.
若四个班种树的平均成活率是90%,全校共种树2000棵,请你估计这些树中,成活的树约有多少棵?
相关知识点
推荐套卷
红星中学开展了“绿化家乡,植树造林 ”活动,并对该校的甲、乙、丙、丁四个班级种树情况进行了考察,并将收集的数据绘制了图①和图②两幅尚不完整的统计图.
请根据图中提供的信息,完成下列问题:
这四个班共种__▲______棵树.
请你补全两幅统计图.
若四个班种树的平均成活率是90%,全校共种树2000棵,请你估计这些树中,成活的树约有多少棵?