在平面直角坐标系中,已知抛物线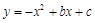 与
与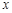 轴交于点
轴交于点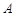 (-1,0)、
(-1,0)、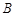 (3,0),与
(3,0),与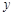 轴的正半轴交于点
轴的正半轴交于点 ,顶点为
,顶点为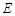 .
.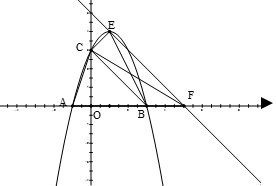
求抛物线解析式及顶点
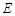 的坐标;
的坐标;如图,过点E作BC平行线,交
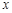 轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: .
轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: .将抛物线向下平移,与
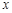 轴交于点M、N,与
轴交于点M、N,与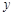 轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
相关知识点
推荐套卷
在平面直角坐标系中,已知抛物线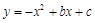 与
与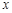 轴交于点
轴交于点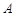 (-1,0)、
(-1,0)、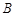 (3,0),与
(3,0),与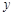 轴的正半轴交于点
轴的正半轴交于点 ,顶点为
,顶点为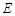 .
.
求抛物线解析式及顶点
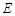 的坐标;
的坐标;如图,过点E作BC平行线,交
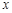 轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: .
轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: .将抛物线向下平移,与
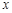 轴交于点M、N,与
轴交于点M、N,与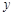 轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式