如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),
与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.求抛物线的函数表达式
求直线BC的函数表达式
点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ=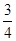 AB时,求tan∠CED的值;
AB时,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标。
相关知识点
推荐套卷
如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),
与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.求抛物线的函数表达式
求直线BC的函数表达式
点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ=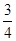 AB时,求tan∠CED的值;
AB时,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标。