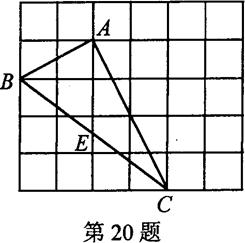
如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题画线段AD// BC且使AD =BC连接CD,且四边形ABCD为格点四边形：
△ACD为____ 三角形，四边形ABCD的面积为___
AC与DB相交于点O，△ABO的面积为____．
—6x+9=(5—2x)
=4y+2
+2
x+1=0
相关知识点
推荐套卷
如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题画线段AD// BC且使AD =BC连接CD,且四边形ABCD为格点四边形：
△ACD为____ 三角形，四边形ABCD的面积为___
AC与DB相交于点O，△ABO的面积为____．
粤公网安备 44130202000953号