如图,已知:等边三角形 的边长为6,点
的边长为6,点 、
、 分别在边
分别在边 、
、 上,且
上,且 . 点
. 点 从点
从点 开始以每秒1个单位长的速度沿射线
开始以每秒1个单位长的速度沿射线 方向运动,设点
方向运动,设点 运动的时间为
运动的时间为 秒. 当
秒. 当 时,直线
时,直线 与过点
与过点 且平行于
且平行于 的直线相交于点
的直线相交于点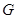 ,
, 的延长线与
的延长线与 的延长线相交于点
的延长线相交于点 ,
, 与
与 相交于点
相交于点
用
 的代数式表示
的代数式表示 ;
;设△
 的面积为
的面积为 ,写出
,写出 与
与 的函数关系式;
的函数关系式;当
 为何值时,点
为何值时,点 和点
和点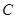 是线段
是线段 的三等分点?
的三等分点?
相关知识点
推荐套卷
如图,已知:等边三角形 的边长为6,点
的边长为6,点 、
、 分别在边
分别在边 、
、 上,且
上,且 . 点
. 点 从点
从点 开始以每秒1个单位长的速度沿射线
开始以每秒1个单位长的速度沿射线 方向运动,设点
方向运动,设点 运动的时间为
运动的时间为 秒. 当
秒. 当 时,直线
时,直线 与过点
与过点 且平行于
且平行于 的直线相交于点
的直线相交于点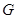 ,
, 的延长线与
的延长线与 的延长线相交于点
的延长线相交于点 ,
, 与
与 相交于点
相交于点
用
 的代数式表示
的代数式表示 ;
;设△
 的面积为
的面积为 ,写出
,写出 与
与 的函数关系式;
的函数关系式;当
 为何值时,点
为何值时,点 和点
和点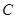 是线段
是线段 的三等分点?
的三等分点?