将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起：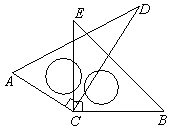
(1)若∠DCE＝35°，则∠ACB的度数为 ▲ °；
(2)若∠ACB＝140°，则∠DCE的度数为 ▲ °；
(3)∠ACB与∠DCE有怎样的数量关系?
(4)三角尺ACD不动，将三角尺BCE的CE边与CA边重合，然后绕点C按顺时针或逆时针方向任意转动一个角度，当∠ACE(0°＜∠ACE＜90°)等于多少度时，这两块三角尺各有一条边互相垂直，直接写出∠ACE角度所有可能的值，不用说明理由．
相关试题
如图，在8×8的网格中，每个小正方形的顶点叫做格点，△OAB的顶点都在格点上，请你在网格中画出一个△OCD，使它的顶点在格点上，且使△OCD与△OAB相似，相似比为2︰1．
抛物线
与y轴交于（0，4）点.
（1）求出m的值；并画出此抛物线的图象；
（2）求此抛物线与x轴的交点坐标；
（3）结合图象回答：x取什么值时，函数值y>0？
，AB=13，CD=12，求AD的长和tanB的值.
，过点C作CD⊥AB于点D，点E为AC上一点，过E点作AC的垂线，交CD的延长线于点F ，与AB交于点G.求证：△ABC∽△FGD
相关知识点
推荐套卷
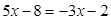粤公网安备 44130202000953号