如图1,若四边形ABCD、四边形CFED都是正方形,显然图中有AG=CE,AG⊥CE.当正方形GFED绕D旋转到如图2的位置时,AG=CE, AG⊥CH是否成立?若成立,请给出证明;若不成立,请说明理由.
当正方形GFED绕D旋转到如图3的位置时,延长CE交AG于H,交AD于M.当AD=4,DG=
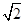 时,求CH的长。
时,求CH的长。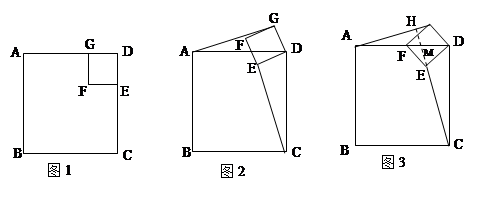
相关知识点
推荐套卷
如图1,若四边形ABCD、四边形CFED都是正方形,显然图中有AG=CE,AG⊥CE.当正方形GFED绕D旋转到如图2的位置时,AG=CE, AG⊥CH是否成立?若成立,请给出证明;若不成立,请说明理由.
当正方形GFED绕D旋转到如图3的位置时,延长CE交AG于H,交AD于M.当AD=4,DG=
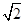 时,求CH的长。
时,求CH的长。