如图①,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.试猜想线段BG和AE的数量关系,请直接写出你得到的结论.
将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图②,通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.
若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,求AF的值.
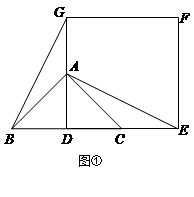

相关知识点
推荐套卷
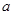 ,
,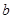 的长方形形纸片的四个角都剪去一个边长为
的长方形形纸片的四个角都剪去一个边长为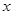 的正方形.(1)用
的正方形.(1)用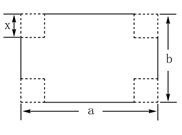
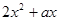
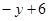
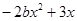
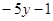 的值与字母
的值与字母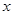 的取值无关,求
的取值无关,求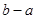 的算术平方根.
的算术平方根.
 是方程
是方程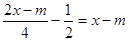 的根,求代数式
的根,求代数式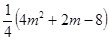
 的值.
的值.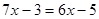


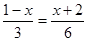
 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号