某公司2011年利润为100万元,因市场竞争,若不开发新项目,预测从2012年起每年利润比上一年减少4万元.2012年初,该公司一次性投入90万元开发新项目,预测在未扣除开发所投入资金的情况下,第n年(n为正整数,2012年为第一年)的利润为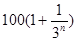 万元.
万元.
(1)设从2012年起的前n年,该公司不开发新项目的累计利润为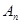 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为 万元(须扣除开发所投入资金),求
万元(须扣除开发所投入资金),求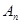 ,
, 的表达式.
的表达式.
(2)依上述预测,该公司从第几年开始,开发新项目的累计利润超过不开发新项目的累计利润?
推荐套卷
某公司2011年利润为100万元,因市场竞争,若不开发新项目,预测从2012年起每年利润比上一年减少4万元.2012年初,该公司一次性投入90万元开发新项目,预测在未扣除开发所投入资金的情况下,第n年(n为正整数,2012年为第一年)的利润为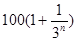 万元.
万元.
(1)设从2012年起的前n年,该公司不开发新项目的累计利润为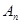 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为 万元(须扣除开发所投入资金),求
万元(须扣除开发所投入资金),求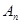 ,
, 的表达式.
的表达式.
(2)依上述预测,该公司从第几年开始,开发新项目的累计利润超过不开发新项目的累计利润?