已知 函数
函数 。
。
(1)求函数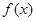 在区间
在区间 上最小值
上最小值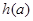 ;
;
(2)对(1)中的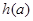 ,若关于
,若关于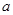 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围;
的取值范围;
(3)若点A ,B
,B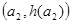 ,C
,C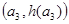 ,从左到右依次是函数
,从左到右依次是函数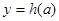 图象上三点,且这三点不共线,求证:
图象上三点,且这三点不共线,求证: 是钝角三角形。
是钝角三角形。
推荐套卷
已知 函数
函数 。
。
(1)求函数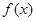 在区间
在区间 上最小值
上最小值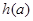 ;
;
(2)对(1)中的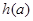 ,若关于
,若关于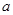 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围;
的取值范围;
(3)若点A ,B
,B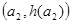 ,C
,C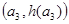 ,从左到右依次是函数
,从左到右依次是函数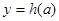 图象上三点,且这三点不共线,求证:
图象上三点,且这三点不共线,求证: 是钝角三角形。
是钝角三角形。