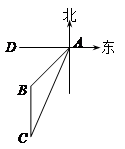一条船上午8点在A处望见西南方向有一座灯塔B(如图),此时测得船和灯塔相距60海里,船以每小时30海里的速度向南偏西24º的方向航行到C处,这时望见灯塔在船的正北方向(参考数据:sin24º≈0.4,cos24º≈0.9)
求几点钟船到达C处
求船到达C处时与灯塔之间的距离.
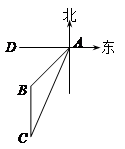
相关知识点
推荐套卷
一条船上午8点在A处望见西南方向有一座灯塔B(如图),此时测得船和灯塔相距60海里,船以每小时30海里的速度向南偏西24º的方向航行到C处,这时望见灯塔在船的正北方向(参考数据:sin24º≈0.4,cos24º≈0.9)
求几点钟船到达C处
求船到达C处时与灯塔之间的距离.