[浙江]2012届浙江宁波初三毕业考试数学试卷
在第六次全国人口普查中,宁波市常住人口约为760万人,其中鄞州区的人口约占18%.则鄞州区人口用科学记数法表示约为( )
| A.0.1368×106人 | B.1.368×105人 | C.1.368×106人 | D.1.36×103 万人 |
一条葡萄藤上结有五串葡萄,每串葡萄的粒数如图所示(单位:粒).则这组数据的中位数为 ( )
| A.37 | B.32 |
| C.35 | D.33.8 |
在平面直角坐标系中,已知点A(-1,0)和B(1,2),连接AB,平移线段AB得到线段A1B1.若点A的对应点A1的坐标为(3,-1),则点B的对应点B1的坐标为( )
| A.(5,3) | B.(5,1) | C.(-1,3) | D.(-1,1) |
已知圆柱的底面直径为4cm,高为5cm,则圆柱的侧面积是 ( )
| A.10cm2 | B.10兀cm2 | C.20兀cm2 | D.40 兀cm2 |
如图,点A的坐标为(- ,0),点B在直线y=x上运动,当线段AB最短时点B的坐为
,0),点B在直线y=x上运动,当线段AB最短时点B的坐为 
A.(- ,- ,- ) ) |
B.(- ,- ,- ) ) |
C.( , , ) ) |
D.(0,0) |
如图,直线l1∥l2,以直线l1上的点A为圆心、适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC.若∠ABC=56º,则∠1= ( )

A.36º B.68º C.72º D.78º
平面直角坐标系中,已知点O(0,0)、A(0,2)、B(1,0),点P是反比例函数 图象上的一个动点,过点P作PQ⊥x轴,垂足为点Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有 ( )
图象上的一个动点,过点P作PQ⊥x轴,垂足为点Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
图①是一瓷砖的图案,用这种瓷砖铺设地面,图②铺成了一个2×2的近似正方形,其中完整菱形共有5个;若铺成3×3的近似正方形图案③,其中完整的菱形有13个;铺成4×4的近似正方形图案④,其中完整的菱形有25个;如此下去,可铺成一个 的近似正方形图案.当得到完整的菱形共221个时,n的值为( )
的近似正方形图案.当得到完整的菱形共221个时,n的值为( )
| A.12 | B.11 | C.10 | D.9 |
中国象棋红方棋子按兵种不同分布如下:1个帅,5个兵,“士、马、车、象、炮”各两个,将所有棋子反面朝上放在棋盘中,任取一个,是象或帅的概率是 .
如图,双曲线 (
( >0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥ 轴,将△ABC沿AC翻折后得△
轴,将△ABC沿AC翻折后得△ ,
, 点落在OA上,则四边形OABC的面积是
点落在OA上,则四边形OABC的面积是 
如图,如下图均为2 2的正方形网格,每个小正方形的边长均为1.请
2的正方形网格,每个小正方形的边长均为1.请
分别在三个图中各画出一个与△ABC成轴对称、顶点在格点上,且位置不同的三角形.
一条船上午8点在A处望见西南方向有一座灯塔B(如图),此时测得船和灯塔相距60海里,船以每小时30海里的速度向南偏西24º的方向航行到C处,这时望见灯塔在船的正北方向(参考数据:sin24º≈0.4,cos24º≈0.9)
求几点钟船到达C处
求船到达C处时与灯塔之间的距离.

某中学为了了解学生体育活动情况,随即调查了720名初二学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”,利用所得的数据制成了扇形统计图和频数分布直方图.根据图示,解答下列问题:若在被调查的学生中随机选出一名学生测试其体育成绩,选出的是“每天锻炼超过1小时”的学生的概率是多少?
“没时间”锻炼的人数是多少?并补全频数分布直方图;
2012年宁波市区初二学生约为2万人,按此调查,可以估计2012年宁波市区初二学生中每天锻炼未超过1小时的学生约有多少万人?
请根据以上结论谈谈你的看法.

某小区准备新建50个停车位,以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位需0.5万元;新建3个地上停车位和2个地下停车位需1.1万元.该小区新建1个地上停车位和1个地下停车位各需多少万元?
若该小区预计投资金额超过10万元而不超过11万元,则共有几种建造方案?
如图,⊙O的直径AB=8,C为圆周上一点,AC=4,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E.
求∠AEC的度数
求证:四边形OBEC是菱形
如图,在平面直角坐标系 中,抛物线
中,抛物线 与
与 轴交于点
轴交于点 ,与
,与 轴交于
轴交于 两点,直线
两点,直线 恰好经过
恰好经过 两点.
两点.求出抛物线
 的解析式,并写出抛物线的对称轴;
的解析式,并写出抛物线的对称轴;点
 在抛物线的对称轴上,抛物线顶点为D若
在抛物线的对称轴上,抛物线顶点为D若 ,求点
,求点 的坐标.
的坐标.





 的根( )
的根( )



 、
、 ,规定
,规定 .若
.若 则
则 的值为( )
的值为( )


 中,自变量x的取值范围_________________________.
中,自变量x的取值范围_________________________. ,垂足为D,若
,垂足为D,若 ,
, , 则DE的长为 .
, 则DE的长为 .
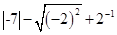 -
-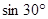
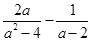 ,其中
,其中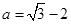

 粤公网安备 44130202000953号
粤公网安备 44130202000953号