（本题8分）已知：△ABC与△EDF都是腰长为9的等腰直角三角形，如图1摆放固定△ABC，将△DEF绕点A顺时针旋转，当DE与AB重合时，旋转中止．在旋转过程中，设DE、DF（或它们的延长线）分别交直线BC于G、H，如图2.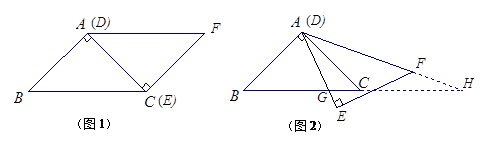
（1）请写出图2中所有与△AGC相似的三角形：________________________________，选择其一说明理由；
（2）当△AGH为等腰三角形时，请直接写出CG的长．
相关试题
，
时，求代数式
的值.
如图，抛物线
＝－
＋5
＋
经过点C（4，0），与轴交于另一点A，与轴交于点B．
（1）求点A、B的坐标；
（2）P是轴上一点，△PAB是等腰三角形，试求P点坐标；
（3）若·Q的半径为1，圆心Q在抛物线上运动，当·Q与轴相切时，求·Q上的点到点B的最短距离．
相关知识点
推荐套卷
粤公网安备 44130202000953号