如图,在正方形的网格图(每小格边长均为1的正方形)中,完成下列各题:
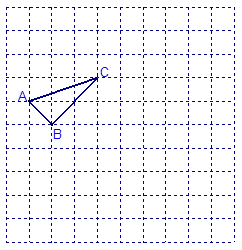
将⊿ABC向右平移4个单位得到⊿A1B1C1;
画出⊿A1B1C1绕点C1逆时针旋转90º所得的⊿A2B2C1;
把⊿ABC的每条边扩大到原来的2倍得到⊿A3B3C3;(顶点画在网格点上).
相关知识点
推荐套卷
如图,在正方形的网格图(每小格边长均为1的正方形)中,完成下列各题:

将⊿ABC向右平移4个单位得到⊿A1B1C1;
画出⊿A1B1C1绕点C1逆时针旋转90º所得的⊿A2B2C1;
把⊿ABC的每条边扩大到原来的2倍得到⊿A3B3C3;(顶点画在网格点上).