如图所示，有两条相交成
角的直路
，
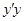，交点是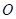
，甲、乙分别在
，
上，起初甲离点
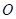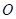km，乙离点
km，后来两人同时用每小时
km的速度，甲沿的方向，乙沿
的方向步行．
⑴起初，两人的距离是多少？
⑵用包含
的式子表示小时后两人的距离；
⑶什么时候两人的距离最短？
相关试题
的值；
的最小值.
中，
，
，
，
∥
，
.
；
的体积.
中，
，
、
、
成等比数列，求数列
.
.
的最小正周期；
上的最大值和最小值.
．
时，过原点的直线与函数
的图象相切于点P，求点P的坐标；
时，求函数
的单调区间；
时，设函数
，若对于
]，
[0，1]
≥
成立，求实数b的取值范围.（
是自然对数的底，
）相关知识点
推荐套卷
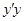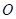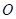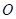如图所示，有两条相交成角的直路，，交点是，甲、乙分别在，上，起初甲离点km，乙离点km，后来两人同时用每小时km的速度，甲沿的方向，乙沿的方向步行．
⑴起初，两人的距离是多少？
⑵用包含的式子表示小时后两人的距离；
⑶什么时候两人的距离最短？
粤公网安备 44130202000953号