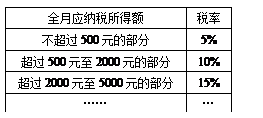
《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过起征点的部分不必纳税,超过起征点的部分为全月应纳税所得额,此项税款按下表分段累进计算:
第十届全国人大常委会第三十一次会议决定,个人所得税起征点自2008年3月1日起由1 600元提高到2 000元.
(1)某公民A全月工资、薪金所得额为3 250,请计算由于个人所得税起征点的调整,该公民A今年三月份的实际收入比二月份多了多少元?
(2)某公民B由于个人所得税起征点的调整,今年三月份的实际收入比二月份多了35元,计算该公民B三月份工资、薪金所得额为多少元?